[ Jocelyn Ireson-Paine's Home
Page
| Publications
| Dobbs Code Talk
Index
| Dobbs
Blog Version
| Facts used in this
tutorial
| Interactive
version of this tutorial on SWISH
| Contact
]
The Prolog Lightbulb Joke
I'm going to explain enough Prolog
for you to understand the
Prolog lightbulb joke.
Prolog stands for "Programming in
Logic". Here is a tiny program,
which asserts a fact and a rule. Together,
these make two-thirds of a well-known syllogism:
is_a( socrates, human ).
is_a( X, mortal ) :-
is_a( X, human ).
Let's read the fact as "Socrates is human": names
starting with a lower-case letter are
constants standing for specific things or
concepts. The rule means
"for any X, X is mortal if X is human". Names
starting with upper-case letters are variables.
To get some action out
of this program, I type it
into a text file. Then I
start a Prolog
interactive shell
and tell it to load this file.
I'll use
Jan Wielemaker's
excellent SWI-Prolog:
Welcome to SWI-Prolog (Multi-threaded, 32 bits, Version 5.6.64)
Copyright (c) 1990-2008 University of Amsterdam.
SWI-Prolog comes with ABSOLUTELY NO WARRANTY. This is free software,
and you are welcome to redistribute it under certain conditions.
Please visit http://www.swi-prolog.org for details.
For help, use ?- help(Topic). or ?- apropos(Word).
1 ?- consult(syllogism).
% syllogism compiled 0.00 sec, 424 bytes
(I've shown my input in bold: Prolog's output,
in normal.)
And then I ask whether the
syllogism's conclusion holds, to which Prolog replies that it does:
2 ?- is_a( socrates, mortal ).
true .
Here are Prolog's replies to some other queries:
3 ?- is_a( socrates, human ).
true .
4 ?- is_a( Person, human ).
Person = socrates .
5 ?- is_a( Person, mortal ).
Person = socrates .
The first query asks Prolog whether
the stated relation holds. The second two
ask it to find some Person —
another variable —
for whom the stated relation holds.
Let's do
some list processing. This is another Prolog program:
borders( belgium, france ).
borders( france, spain ).
borders( germany, austria ).
borders( germany, denmark ).
borders( germany, switzerland ).
borders( netherlands, belgium ).
borders( netherlands, germany ).
borders( spian, portugal ).
route( A, B ) :-
borders( A, B ).
route( A, B ) :-
borders( A, Z ),
route( Z, B ).
I'll interpret the first rule as:
there is a route from A to B if
A borders B. The second, as:
there is a route from A to B if
A borders some Z,
and there is a route from that
Z to B.
In 2002, I took a train from
Maastricht in Holland to Braga in Portugal: I'd been watching the
Euro-welcoming ceremony in Maastricht, and
wanted to get from there to Portugal by
1 pm on the following Saturday to
see how the
market-stall holders in Braga's first post-Euro
market were coping with the changeover.
If this seems perverse, let's just say that
I'd stayed in Braga before, and knew that the
town market closed at 1 pm each Saturday.
Let's
ask Prolog whether the route itself is feasible:
advanced readers can augment
my program with train timetables and
work out a minimum journey time.
So I put the above
program into a file
called "countries" and ask the interactive shell:
6 ?- consult(countries).
% countries compiled 0.00 sec, 408 bytes
7 ?- route(netherlands,portugal).
false.
What's that? There's no such route? Must be something
wrong with my code. Oh, I see: I mistyped "spain" as
"spian" in the above file. So Prolog couldn't infer a route
from the facts, and replied "false". Some Prologs
don't reply "false", but "no". It means the same:
no answer can be proven. This kind of thing can
happen in other ways. For example,
if I'd typed "broders" instead of "borders" in one of those
facts, "route" would have ignored it, and my
query would have answered "false" in the same
way.
Now I've edited "spian" to "spain", and I'm going
to reload my facts and ask again whether there's
a route:
8 ?- consult(countries_2).
% countries compiled 0.00 sec, 408 bytes
9 ?- route(netherlands,portugal).
true .
And this time, Prolog tells me that there is.
But what is that route? Here's an amended
definition
of "route" that will calculate it for me:
route( A, B, [ go(A,B) ] ) :-
borders( A, B ).
route( A, B, [ go(A,Z) | ZtoB ] ) :-
borders( A, Z ),
route( Z, B, ZtoB ).
Now, I've given "route" an extra,
third, argument. I intend this to be
an output argument, analogous to the
result of a function: "route"
will put something into it. The first
clause for "route" puts "[ go(A,B) ]" into it.
This is a one-element list. The square brackets
say it's a list, and its single element
is "go(A,B)". Logicians and
Prolog programmers call "go(A,B)" a "term". It's like
a structure or record, with two fields, distinguished
by position rather than by name. The first field will
become whatever A holds; the second, whatever B holds.
Whenever possible,
Prolog programmers read programs as
sets of logical statements, not as
commands. So here's a logical
reading for the first clause for "route": if A borders B,
the route from
A to B is the list containing the record "go(A,B)".
And here's a logical reading for
the second clause: if A borders some Z, and
there's a route ZtoB from Z to B, then
the route from
A to B is the list holding
the record "go(A,Z)" followed by ZtoB. Square brackets
indicate a list, as before; vertical bar means "followed by".
Could recursion ever be more concise?
10 ?- consult(countries_3).
% countries compiled 0.00 sec, 408 bytes
11 ?- route(netherlands,portugal,R).
R = [go(netherlands, belgium), go(belgium, france),
go(france, spain), go(spain, portugal)]
This "route" predicate generates a list, putting
it into an output argument. But predicates can also
take lists as inputs, as I'll show now. A textbook author —
possibly Patrick Henry
Winston — once wrote the
following as an example to help novices
understand recursion:
This is how to tidy up your room:
if there are no toys lying around,
do nothing.
if there is a toy lying around,
pick it up and put it in the toybox,
and tidy up your room.
To render this as Prolog.
I'll write a predicate called "tidy" with
two arguments. The first, an
input, will be a list of toys.
The second, an output, will be a list of the commands
a robot must obey in order to tidy them.
Here's my predicate:
tidy( [], [] ).
tidy( [ Toy | OtherToys ], [ pick_up(Toy), move_to(toybox), drop(Toy) | OtherCommands ] ) :-
tidy( OtherToys, OtherCommands ).
I'll read the first clause as meaning:
if the list of toys to tidy is empty,
the list of commands needed is empty.
And the second as: if the list of toys starts
with any toy (a variable) which we'll call Toy, and
continues with OtherToys, and
the commands needed to tidy OtherToys are
OtherCommands, then
the complete list of commands needed is "pick_up(Toy)" followed
by "move_to(toybox)" followed by "drop(Toy)" followed by
OtherCommands.
Let's test this:
12 ?- consult(tidy).
% tidy compiled 0.00 sec, 864 bytes
13 ?- tidy( [ teddy, ball, golly, bat ], Cmds ).
Cmds = [pick_up(teddy), move_to(toybox), drop(teddy),
pick_up(ball), move_to(toybox), drop(ball),
pick_up(golly), move_to(toybox), drop(golly),
pick_up(bat), move_to(toybox), drop(bat)]
What this shows is that although Prolog has its roots
in logical inference, it can
do the same kind of list processing as any other language.
And in doing so, can
build huge data structures indeed.
I have just given my Prolog system this
query and received the following reply:
14 ?- length( L, 5000000 ).
L = [_G8, _G11, _G14, _G17, _G20, _G23, _G26, _G29, _G32|...].
The predicate
"length" is a built-in, which can measure the
length of a list. Or if given an integer as input, return
a list of the specified length. Here, L has become
a list containing
5,000,000 elements, of which
Prolog has shown me 9, indicating the rest as dots.
I got an out-of-stack error when
I asked for 6,000,000, but hey, 5 million ain't bad.
Here's another vast structure which I've managed to
provoke by using the Prolog debugger on my
category
theory demonstrations:
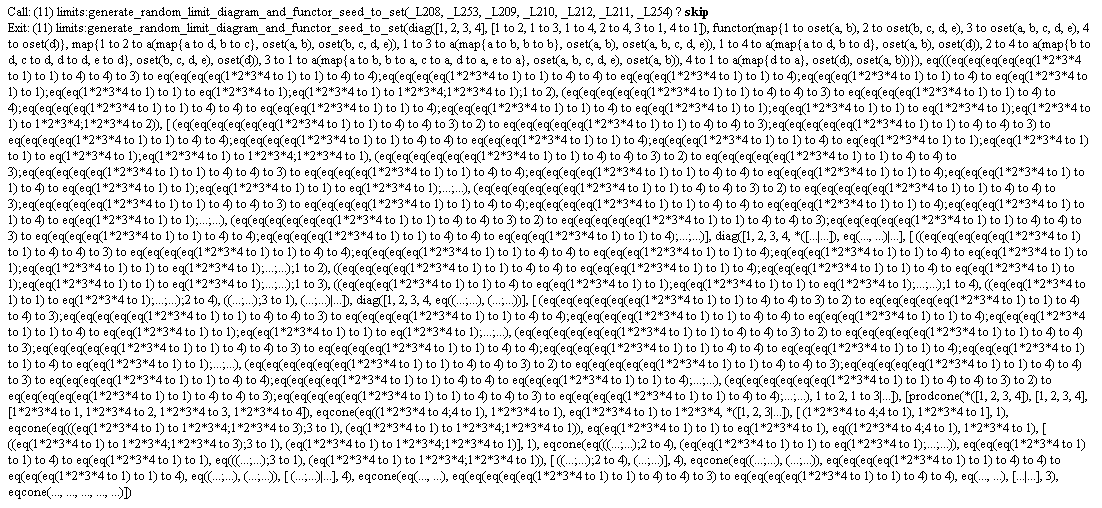 Now, because I wrote the program, I know the term isn't nearly as big as that
5-million long list. But I also know it contains many internal links that
point into the same subterms. Every time Prolog
displays one of these links, it displays the
subterm at the end of it, even if it has done so
a hundred times already. This makes sense in the context of logic programming,
where two terms are equal if they contain identical values, regardless of
whether these are the same place in memory.
But it also means that unless I write special code to detect
common subterms and display them once only, I get
swamped by debugging output.
Now, because I wrote the program, I know the term isn't nearly as big as that
5-million long list. But I also know it contains many internal links that
point into the same subterms. Every time Prolog
displays one of these links, it displays the
subterm at the end of it, even if it has done so
a hundred times already. This makes sense in the context of logic programming,
where two terms are equal if they contain identical values, regardless of
whether these are the same place in memory.
But it also means that unless I write special code to detect
common subterms and display them once only, I get
swamped by debugging output.
So it's 2 am.
You are debugging a
Prolog program. You slump before your
screen, glazed eyes staring into a data structure that's as opaque as the
programmer-fuel coffee in your cup and the
night sky you see from your office window.
Somewhere in your 30 modules and 30,000 lines
of code is a misspelt constant or
a misspelt predicate. You can't
think of anything else to do, so you run
your program again, hoping it will automagically
have healed:
How many Prolog programmers does it take to change a lightbulb?
false.
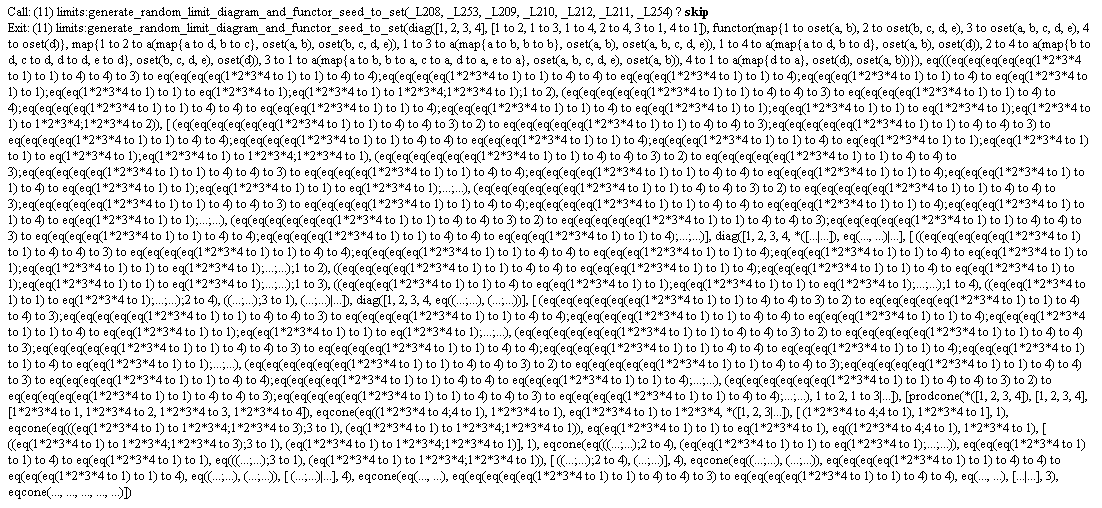 Now, because I wrote the program, I know the term isn't nearly as big as that
5-million long list. But I also know it contains many internal links that
point into the same subterms. Every time Prolog
displays one of these links, it displays the
subterm at the end of it, even if it has done so
a hundred times already. This makes sense in the context of logic programming,
where two terms are equal if they contain identical values, regardless of
whether these are the same place in memory.
But it also means that unless I write special code to detect
common subterms and display them once only, I get
swamped by debugging output.
Now, because I wrote the program, I know the term isn't nearly as big as that
5-million long list. But I also know it contains many internal links that
point into the same subterms. Every time Prolog
displays one of these links, it displays the
subterm at the end of it, even if it has done so
a hundred times already. This makes sense in the context of logic programming,
where two terms are equal if they contain identical values, regardless of
whether these are the same place in memory.
But it also means that unless I write special code to detect
common subterms and display them once only, I get
swamped by debugging output.